Home >> Blog >> Formulas for Spiral Wound Wave Springs
Formulas for Spiral Wound Wave Springs
Nomenclature
T = Thickness of Material [mm]
SW = Radial Width of Material, [mm] F = Load, [N]
W.H. = Work Height, [mm]
H = Free height, [mm]
N = Number of Turns
Z = Number of Waves per turn
OD = Outside Diameter, [mm]
ID = Inside Diameter, [mm]
Dm= Mean Diameter, * [mm]
B = Deflection [mm]
σ = Operating Stress [N/mm2]
E = Modulus of Elasticity, [N/mm2]
K = Wave Factor**
*Mean Diameter Dm = [(OD + ID):2]
***Wave Factor K:
|
Number of Waves per turn [Z]: |
2.0-4.0 |
4.5-6.5 |
7.0-9.5 |
≥10.0 |
|
Wave Factor [K]: |
3.88 |
2.90 |
2.30 |
2.13 |
Diameter Expansion
The diameter of a flat wire wave spring increases when compressed in the axial direction. The following formula is an example of its maximum achievable outside diameter when compressed at the block level.
R = Wave Radius*1 [mm]
SW = Radial Width of Material [mm]
X = 1/2 Wave Frequency*3
H = Free Height [mm]
Z = Number of waves per Turn
θ = Angle, degrees*2 [Grad]
Y = Mean Free Height*4 [mm]
T = Thickness of Material [mm]
*1 Wave Radius R = [(4Y2+ X2) : 8Y]
*2 Angle Ð = [ArcSin (X : 2R)]
*3 1/2 Wave Frequency X = [π · Dm : 2Z]
*4 Mean Free Height Y = [(H-T):2]
Max. outside diameter at 100% deflection = 0.02222 · R · Z · θ + SW
Single-Turn Wave Spring With Gap or Overlap
The operating stress of a single turn wave spring should never exceed the minimum tensile strength of the flat wire material. Keep deflection between 30 and 70%.
Deflection B = F · K · Dm3 . ID
. E · SW · T3· Z4 OD
Operating Stress σ = 3·π·F·Dm
. 4 · SW · t 2· Z2
Multi-Turn Wave Springs
The operating stress of a single turn wave spring should never exceed the minimum tensile strength of the flat wire material. Keep deflection between 20 and 80%.
Deflection B = F · K · Dm3 . ID
. E · SW · T3· Z4 OD
Operating Stress σ = 3·π·F·Dm
. 4 · SW · t 2· Z2
Nested Multi-Turn Wave Springs
The operating stress of a single turn wave spring should never exceed the minimum tensile strength of the flat wire material. Keep deflection between 30 and 70%.
Deflection B = F · K · Dm3 . ID
. E · SW · T3 · Z4 · N OD
Operating Stress σ = 3·π·F·Dm
. 4 · SW · t 2· Z2 · N
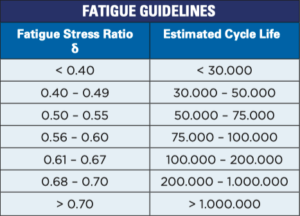
Fatigue Stress Ratio
Calculating the ratio between WH12 and WH2 can determine the required number of load cycles. The results are then compared to the guideline table values to figure out final number.
δ = Fatigue Stress Ratio
σ = Material tensile strength [N/mmÐ]
σ = Calculated operating stress at lower work height [N/mm2]
σ 2= Calculated operating stress at upper work height [N/mm2]
Fatigue Stress Ratio δ = (σMat – σ1)
. (σMat – σ2)
To learn about selecting the correct products for your operating environment please contact your local Daemar Technical Sales Representative.
















